소리의 합성(인간과 소리 3강) - 사인파의 수리적 기초
1) 사인파의 수리적 표현
수식 : 개념을 분명하고 간결하게 나타낼 수 있는 방법
x(t) 라고 나타낸 함수 : t 의 함수 x, t에 따라 변하는 x
시간에 따라 변하는 어떤 결과
2) 사인파 가지고 놀기
x(t) = A·sin(2πft + ø)
(A : 크기 또는 진폭, f : 주파수, ø : 위상)
A(진폭 Amplitude)의 크기가 클수록 사인파의 마루와 골이 크게 나타남
f(주파수 Frequency)의 크기가 클 수록 단위 시간안에 많은 사이클이 나타남
ø(위상 Phase)값에 따라 사이클의 시작 지점이 달라짐
3) 사인파의 변조
이상적인 사인파와는 달리 보통 진폭이 갈수록 줄어든다.
대부분의 파동은 시간에 따라 진폭 및 주파수가 변함
1을 더하면 모든 값(파형)이 위로 한칸 올라감
x를 더하면 시간이 지날수록 위로 올라감 (sin 밖에)
x를 곱하면 갈수록 진폭이 커짐 (sin 밖에)
x로 나눠주면 갈수록 진폭이 작아짐 (sin 밖에)
주파수를 다르게 곱한 것을 더하면 진폭이 증가와 감소를 반복함 (비트)
x를 곱하면 갈수록 주파수가 커짐 (sin 안쪽에)
주파수-x^5 을 하면 주파수가 점점 감소
'소리-공기 연구소' 카테고리의 다른 글
| 해양 - 한국의 동해 (0) | 2014.02.15 |
|---|---|
| 음악이 사람의 습관을 바꿀 수 있을까 ? (0) | 2013.10.01 |
| 블루골드, 물 이야기 - 문명에서 농업용수까지 - (0) | 2012.10.28 |
| 물을 둘러싼 환경의 변화, 'Blue Gold' 시대 도래 - 물산업분야 (0) | 2012.10.22 |
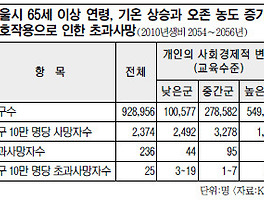
| 암울한 50년 후 서울, 숨쉬기 힘들어 사망 증가… KEI 기후변화 보고서 (0) | 2012.08.24 |
| 공기청정기, 환기, 공기질, 환경 관련 싸이트 정리 (0) | 2012.08.09 |
| 실내 공기에 관련된 유용한 그림들~ (0) | 2012.07.06 |
| 소리의 생성과 인식 (0) | 2012.06.01 |
취업, 창업의 막막함, 외주 관리, 제품 부재!
당신의 고민은 무엇입니까? 현실과 동떨어진 교육, 실패만 반복하는 외주 계약,
아이디어는 있지만 구현할 기술이 없는 막막함.
우리는 알고 있습니다. 문제의 원인은 '명확한 학습, 실전 경험과 신뢰할 수 있는 기술력의 부재'에서 시작됩니다.
이제 고민을 멈추고, 캐어랩을 만나세요!
코딩(펌웨어), 전자부품과 디지털 회로설계, PCB 설계 제작, 고객(시장/수출) 발굴과 마케팅 전략으로 당신을 지원합니다.
제품 설계의 고수는 성공이 만든 게 아니라 실패가 만듭니다. 아이디어를 양산 가능한 제품으로!
귀사의 제품을 만드세요. 교육과 개발 실적으로 신뢰할 수 있는 파트너를 확보하세요.
캐어랩